고등학교 인공지능 수학 수업자료 3 (유사도 란?)
고등학교 인공지능 수학수업자료3
단원II 텍스트 자료의 표현과 분류 - 텍스트 자료의 분류
이 단원은 인공지능을 이용하여 텍스트를 분류하는 수학적 방법을 이해함을 학습목표로 하고 있다. 벡터화한 두 개의 데이터(단어 또는 문장 또는 기타 자료 등) 의 유사한 정도를 수치화한 것을 유사도 라고 하는데 고등학교 인공지능 수학 교과에서는 보통 유클리드 거리, 코사인 유사도, 자카드 유사도 정도 를 다루고 있다. 교과서별 차이가 있는데 예를들어 미래엔 교과서의 경우 이 세 유사도를 모두 다루고 있으나, 천재교과서의 경우 유클리드 거리만 다룬다. 다루는 개념이 적다고 천재교과서가 안 좋다는 것은 아니다. 아마 인공지능 수학이 고등학교 1학년 수학 만 다루고 배울 수 있는 교과이기에 교과서를 집필하는 교수님과 선생님들도 어디까지 내용을 다룰지에 대한 고민이 있었 것이라 생각하다.
유클리드 거리란?
3 차원 이하 사이의 공간에서는 직관적으로 두점사이의 거리로 정의된다.
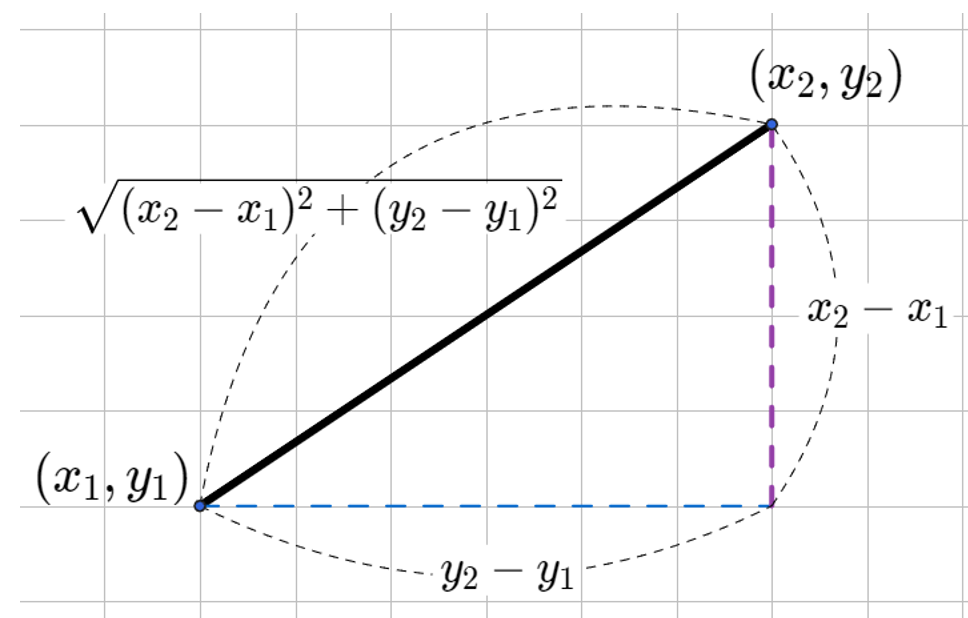
이를 성분이 n개인 데이터(벡터) 로 확장하면 아래와 같이 정의할 수 있다.
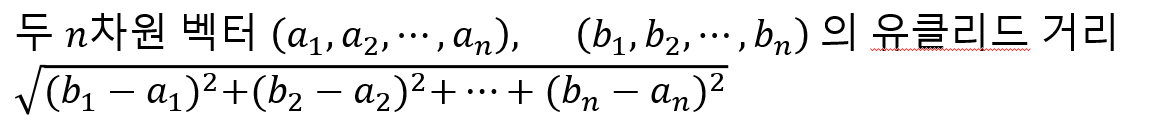
유클리드 거리가 0에 가까울 수록 유사도가 높다고 말할 수 있으며 개념이 직관적이기에 고1 수학을 이수한 학생들에게 설명하기에 큰 무리는 없다.
코사인 유사도란?
예를들어 다음 세 문서에서 (강원도, 양양, 속초) 가 언급된 수를 셈하여 수치화(벡터화) 한다고 하자.
문서1 = 강원도 양양에 한 수학교사
문서2 = 강원도 양양의 수학교사 남궁연, 그는 강원도 양양을 사랑한다.
문서3 = 남궁연은 속초에서 처음 근무를 시작했다.
이를 수치화하면 문서1 = (1,1,0) , 문서2 = (3,3,0), 문서3= (0,0,1) 이다. 문서1과 문서3의 유클리드 거리가 적다고 해서 문서1과 문서3이 문서1과 문서2 보다 더 유사하다고 말하기에는 무리가 있다. 이렇듯 수치화 한 데이터에 따라 사용하기에 적절한 유사도는 다르고, 코사인 유사도는 벡터 의 크기가 아닌 벡터의 방향으로 두 자료의 유사도를 판단한다.
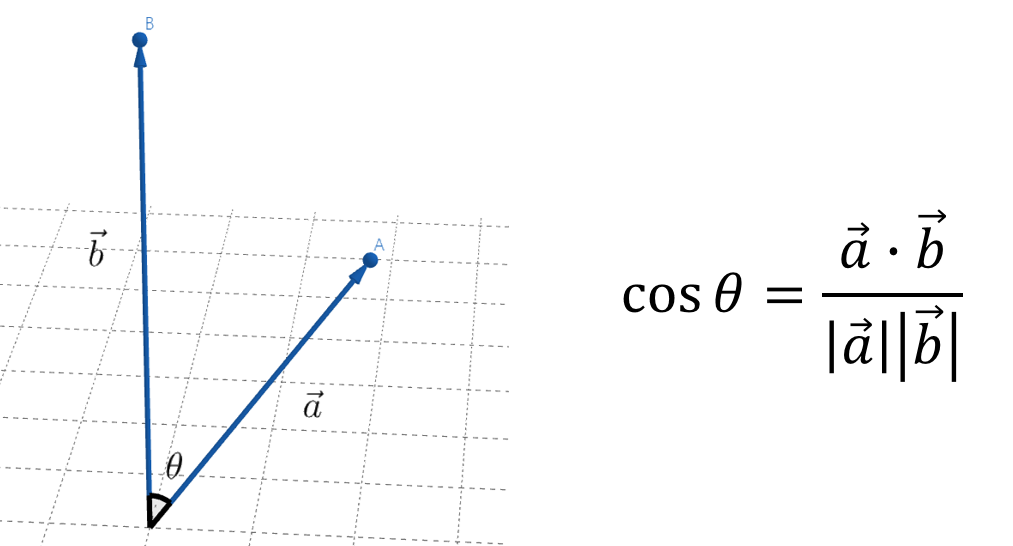
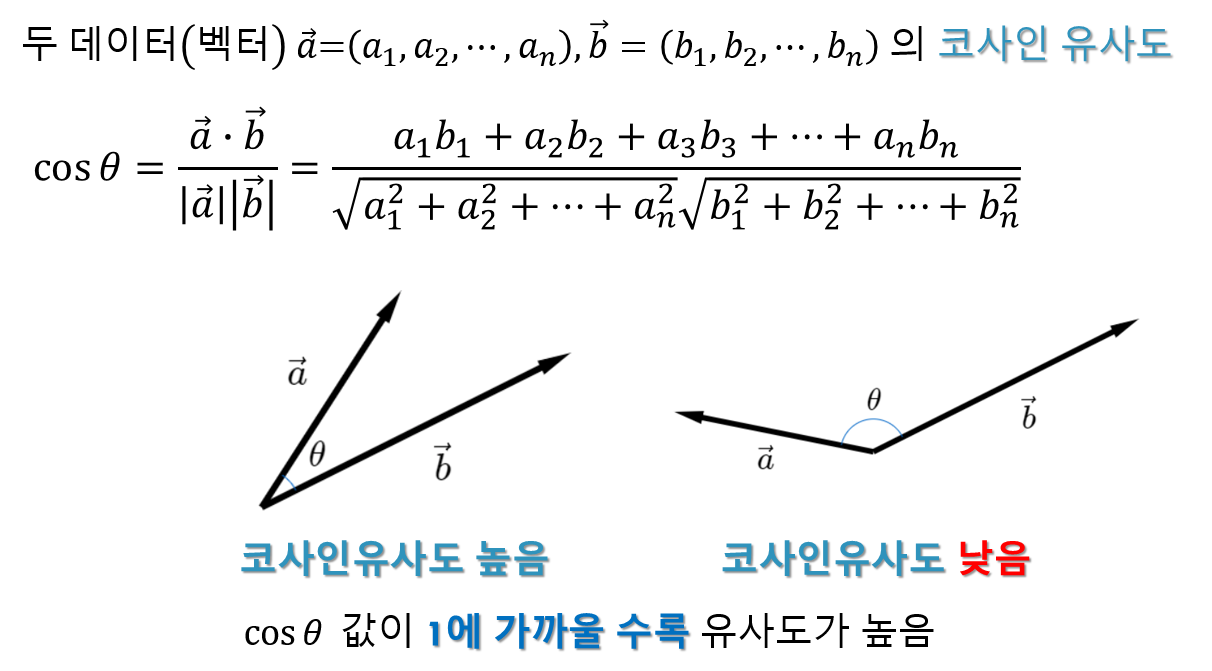
단, 고1 수학만 배운 학생들은 두 벡터의 내적, 고등학교 삼각함수를 배우지 않았기에 지도 하기에 어려움이 있을 수 있다. 나는 이런 학생을 대상으로 수업을 진행한다면 공학도구를 이용하여 그냥 직관적으로 내적이 성분의 곱의 합이랑 일치함을 간단히 보여주고 넘어가려고 한다. (이에 대한 내용 추가해야 함)
두 자료의 코사인 유사도는 결과값이 코사인값이기에 -1 에서 1사이로 나오며, 세타의 값이 0일 수록 두 벡터의 방향이 유사하다고 말할 수 있기에 코사인 유사도(코사인값)는 1에 가까울 수록 두 자료의 유사도는 크다.
유사도 단원에 나오는 교과서 문제를 보면 아래와 같다
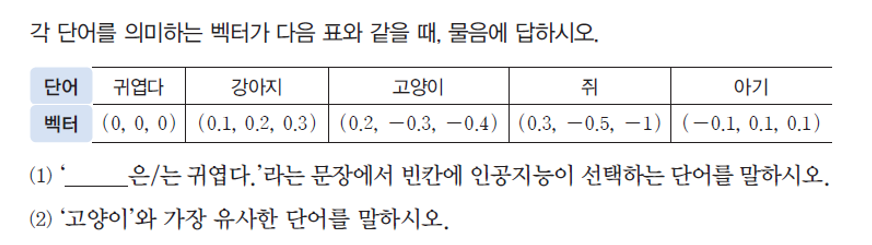
유사도에 대한 계산 연습은 할 수 있지만, 그래도 명색이 인공지능 수학 교과 인데 이런 정도의 단순 계산 문제만 풀고 넘어가기에는 아쉽다. 이런 단순 계산은 컴퓨터에게 시키면 된다. 그래서 유사도를 이용하여 관련된 실제 자료를 분석하고 분류해보는 수업을 나름 기획(?) 하였고, 연수 전날 급하게 생각한 것이긴 하지만 나름 잘 구성된 수업 같다. 이를 다음 포스트에서 설명하고자 한다.
댓글
댓글 쓰기